#statusMessage#
Möchten Sie den Produktvergleich starten?

Die Netzwerkanalyse kommt z. B. bei Stabilitätstests, zur Bauteilecharakterisierung oder zur Messung des Frequenzgangs zum Einsatz. Typische Anwendungen mit dem Vektor-Netzwerkanalysator (VNA) sind z. B. die Einfügedämpfung von Filtern oder die Übertragungseigenschaften von Verstärkern. Im Folgenden erhalten Sie einen Überblick über die grundlegenden Prinzipien der Netzwerkanalyse einschließlich relevanter HF-Grundlagen zum Thema Übertragungsleitung oder Smith-Diagramm.
Ein Vektor-Netzwerkanalysator (VNA) misst die reflektierten und übertragenen Anteile eines Signals, das in eine Übertragungsleitung eingekoppelt, auf der Übertragungsleitung zur Quelle zurück reflektiert (aufgrund einer Impedanz-Fehlanpassung) und effektiv zur Empfängerkomponente, z. B. eine Antenne, übertragen wird.
Netzwerkanalysatoren senden über einen integrierten Signalgenerator ein Signal mit bekannter Frequenz, Amplitude und Phase an einen Prüfling. Die Anregung der Schaltung wird gemessen; man erhält die sog. Streuparameter (S-Parameter). Der Prüfling reflektiert einen Teil dieses Signals. Die übrigen Signalanteile erreichen das Messobjekt, werden dort verändert (gedämpft, verstärkt, phasenverschoben, gemischt) und treten am DUT-Ausgang als übertragenes Signal aus. Durch Fehlanpassung an die Last kann auch hier wieder ein Teil des transmittierten Signals reflektiert werden.
Die effiziente Leistungsübertragung ist eine grundlegende Anforderung an Kommunikationssysteme. Um HF-Signale störungsfrei zu übertragen oder zu empfangen, müssen die Impedanzen der Übertragungsleitungen, Antennen, Verstärker etc. korrekt mit der Signalquelle abgeglichen werden. Impedanz-Fehlanpassungen treten auf, wenn die Real- und Imaginäranteile der Eingangs- und Ausgangsimpedanzen zwischen zwei verbundenen Geräten nicht ideal sind.
Signalverzerrungen in einem Kommunikationssystem können zum einen durch nichtlineare Effekte entstehen, wenn beispielsweise Intermodulationsprodukte aus gewünschten Trägersignalen erzeugt werden. Aber auch lineare Systeme können Signalverzerrungen verursachen, indem sie die Amplituden- oder Phasenbeziehungen innerhalb des Frequenzspektrums eines Signals beeinflussen.
Sowohl aktive als auch passive nichtlineare Geräte können ein Eingangssignal in der Frequenz verschieben oder andere Frequenzkomponenten hinzufügen, z. B. Oberwellen und Störsignale.
Beispiel für nichtlinear induzierte Verzerrung: Wird ein Verstärker eingangsseitig ausgesteuert, übersteuert das Ausgangssignal, weil der Verstärker gesättigt ist. Das Ausgangssignal ist keine reine Sinuskurve mehr. Es treten Oberwellen auf, die ein Vielfaches der Eingangsfrequenz betragen. Passive Systeme können bei hohen Leistungspegeln ebenfalls ein nichtlineares Verhalten aufweisen, z. B. ein LC-Filter, das Induktoren mit Magnetkern verwendet. Magnetische Materialien weisen oft Hysterese-Effekte auf, die nichtlinear sind.
Abb.: nichtlinear induzierte Verzerrung
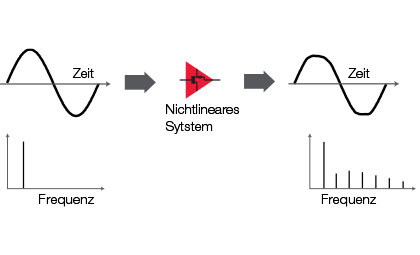
Bei linearen Geräten werden die Eingangssignale im Betrag (Amplitude) oder in der Phase verändert. Die Eingangs- und Ausgangsfrequenzen sind identisch; es werden keine zusätzlichen Frequenzen oder neuen Signale erzeugt. Für eine lineare, verzerrungsfreie Signalübertragung muss der Amplitudengang des Prüflings (engl. DUT, device under test) flach und der Phasengang über die gewünschte Bandbreite linear sein.
Beispiel für linear induzierte Verzerrung: Ein Rechtecksignal mit hochfrequenten Anteilen passiert ein lineares Bandpassfilter, das ausgewählte Frequenzen mit geringer Dämpfung durchlässt. Auch wenn der Filter eine lineare Phasenleistung aufweist, werden die Komponenten außerhalb des Frequenzbandes gedämpft, so dass ein Ausgangssignal übrigbleibt, das eher sinusförmig ist. Wird dasselbe Rechteck-Eingangssignal durch einen linearen Filter geleitet, der nur die Phase der dritten Harmonischen invertiert, die Amplituden aber unverändert lässt, ist das Ausgangssignal eher impulsförmig.
Abb.: Änderung der Amplitude mit der Frequenz
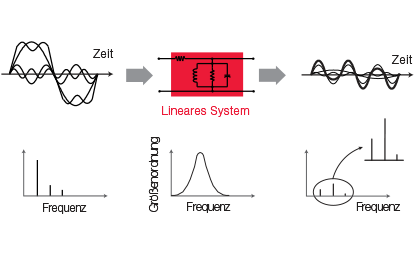
Um ein lineares Netzwerk vollständig zu charakterisieren und eine verzerrungsfreie Signalübertragung zu gewährleisten, müssen Amplituden- und Phasengang ermittelt und komplexe Impedanzmessungen durchgeführt werden. Auch Entwicklungsingenieure für computergestützte Schaltungs-Simulationsmodelle (engl. CAE, computer aided engineering) benötigen präzise Amplituden- und Phasenwerte der in den Schaltungen verwendeten Komponenten. Für eine Charakterisierung im Zeitbereich ist darüber hinaus die inverse Fourier-Transformation erforderlich. Diese basiert auf dem Amplituden- und Phasengang.
Die Messgenauigkeit kann über eine sog. Vektorfehlerkorrektur verbessert werden, indem die Auswirkungen inhärenter Messsystemfehler beseitigt werden. Ein effektives Fehlermodell erfordert präzise Amplituden- und Phaseninformationen.
Das Smith-Diagramm ist eine typische Darstellung der Messergebnisse. Mit dessen Hilfe lässt sich die Stabilität bzw. die Schwingfestigkeit einer Schaltung feststellen. Das Systemverhalten in der Nähe der Schwinggrenze (Polstellen) liefert relevante Informationen für das Systemdesign. Dieses darf durch eine Anregung (z. B. ein Störimpuls) nicht selbstständig beginnen zu schwingen, was einem Systemausfall entspräche.
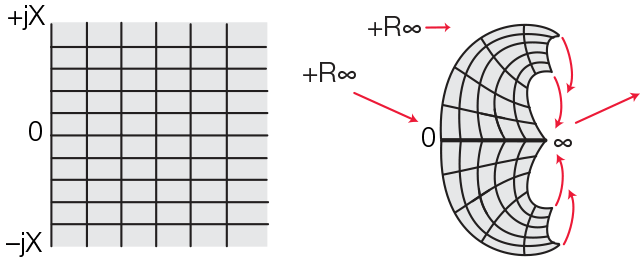
Die Reflexion eines Signals hängt von der Impedanz ab, die das einfallende Signal "sieht". Jede Impedanz lässt sich durch einen Real- und einen Imaginäranteil darstellen (R + jX) und in Form eines geradlinigen Gitters abbilden. Ein offener Stromkreis erscheint auf der Achse im Unendlichen und kann daher nicht dargestellt werden.
Abb.: geradlinige Impedanzebene und Impedanzebene als Polardiagramm
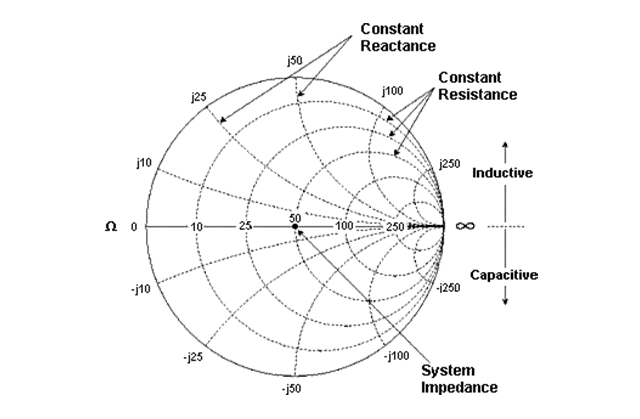
Die positive Hälfte der Impedanzebene stellt das sog. Smith-Diagramm dar. Auf dem Smith-Diagramm erscheint ein konstanter Widerstand als Kreis; Blindwiderstände erscheinen als Bögen. Die Impedanzen im Smith-Diagramm sind immer auf die charakteristische Impedanz des betreffenden Bauteils oder Systems normiert, in der Regel auf 50 Ohm für HF-Systeme. Die Mitte des Diagramms repräsentiert die ideale Signalverbindung
Abb.: Exemplarisches Smith-Diagramm und dessen Interpretation
Die Verbindung zwischen zwei Geräten muss perfekt aufeinander abgestimmt sein, damit eine maximale Signalleistung an eine Last übertragen werden kann. D. h. die Ausgangsimpedanz RS einer Quelle und die Eingangsimpedanz RL einer Last müssen optimal abgeglichen sein. Diese Bedingung ist erfüllt, wenn RL = RS ist, unabhängig davon, ob der Stimulus von einer Gleichspannungsquelle oder von HF-Sinuswellen stammt. Ist die Quellenimpedanz kein reiner ohmscher Widerstand, so erfolgt die maximale Leistungsübertragung, wenn die Lastimpedanz gleich der konjugierten komplexen Impedanz der Quelle ist. (Beispiel: Wenn RS = 0,6 + j 0,3 ist, dann lautet die komplexe Konjugation RS* = 0,6 - j 0,3.)
Abb.: Die optimale Signalübertragung erfolgt, wenn RL = RS ist.
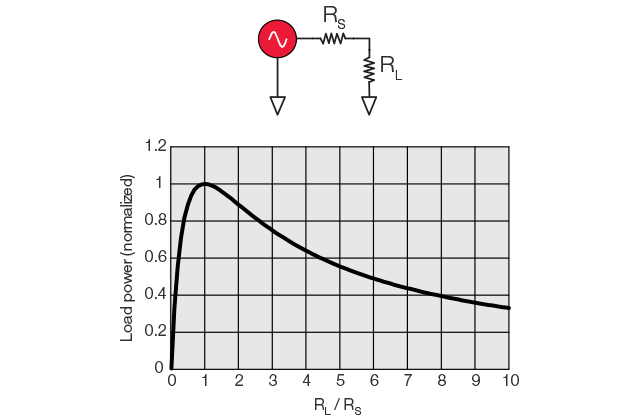
Die Signalübertragung durch ein Übertragungsmedium lässt sich mit Wanderwellen vergleichen. Bei sehr niedrigen Frequenzen, d. h. bei größeren Wellenlängen, reicht hierfür ein einfacher Draht. Sein Widerstand ist verhältnismäßig gering und die Auswirkung auf niederfrequente Signale kann vernachlässigt werden. Höhere Frequenzen erfordern eine hochwertige Übertragungsleitung mit einem passenden Abschlusswiderstand. Der Abschluss absorbiert die eintreffenden Signale und verhindert eine ungewollte Reflexion. Wird die Leitung mit einem Widerstand terminiert, der der Wellenimpedanz entspricht, erfolgt eine optimale Signalübertragung. Entspricht der Abschluss nicht dem Wellenwiderstand, werden Signalanteile zur Quelle zurück reflektiert.
Bei einem Kurzschluss, d. h. es wird keine Spannung aufrechterhalten, verläuft eine reflektierte Welle entlang der Leitung zurück zur Quelle. Die reflektierte und die einfallende Spannungswelle haben jeweils den gleichen Betrag, bewegen sich aber in entgegengesetzte Richtungen. Bildet die Übertragungsleitung einen offenen Stromkreis, ist die reflektierte Stromwelle um 180 Grad phasenverschoben zur einfallenden Welle, während die reflektierte Spannungswelle auf Höhe der Last phasengleich zur eintretenden Spannungswelle verläuft. Dies garantiert, dass der Strom an der offenen Stelle gleich Null ist. Die reflektierte und die einfallende Stromwelle haben jeweils die gleiche Amplitude, laufen aber in entgegengesetzte Richtungen.
In beiden Fällen, Kurzschluss und offener Stromkreis, bildet sich auf der Übertragungsleitung ein stehendes Wellenmuster aus. Die Spannungstäler sind gleich Null und die Spannungsspitzen sind doppelt so groß wie die einfallende Spannung.
Der Abschluss einer 50-Ohm-Übertragungsleitung mit einem 25-Ohm-Widerstand führt zu einem Zustand zwischen vollständiger Absorption und vollständiger Reflexion führt, d. h. ein Teil der einfallenden Leistung wird absorbiert und ein Teil wird reflektiert. Die Amplitude der reflektierten Spannungswelle beträgt ein Drittel der Amplitude der einfallenden Welle. Beide Wellen sind auf Höhe der Last um 180 Grad phasenverschoben. Die Täler des Stehwellen-Musters betragen nicht mehr Null, und die Peaks sind kleiner als beim Kurzschluss und im offenen Fall. Das Verhältnis zwischen den Peaks und den Tälern beträgt 2:1.
Moderne Vektor-Netzwerkanalysatoren messen die einfallenden und reflektierten Wellen direktwährend eines Frequenzdurchlaufs. Die Impedanzergebnisse können in verschiedenen Formaten einschließlich der VSWR (voltage standing wave ratio) angezeigt werden.
Die Netzwerkanalyse bezeichnet allgemein die Messung einer einfallenden Welle mit dem R-bzw. Referenzkanal. Die reflektierte Welle wird mit dem A-Kanal gemessen und die übertragene Welle wird mit dem B-Kanal gemessen. Mit den Amplituden- und Phaseninformationen dieser Wellen lassen sich die Reflexions- und Übertragungseigenschaften eines Prüflings quantifizieren. Die Reflexion und Transmission können als vektorielle (Betrag und Phase), skalare (nur Betrag) oder nur phasenbezogene Größen dargestellt werden. Beispielsweise stellt die Rückflussdämpfung eine skalare Messung der Reflexion dar, während die Impedanz eine vektorielle Reflexionsmessung ist.
Um ein unbekanntes lineares System mit zwei Anschlüssen vollständig zu charakterisieren, müssen wir Messungen unter verschiedenen Bedingungen durchführen und eine Reihe von Parametern berechnen. Diese Parameter können das elektrische Verhalten unseres Systems, d. h. unseres Netzwerks, vollständig beschreiben, auch unter variierenden Quellen- und Lastbedingungen.
Abb.: Terminologie bei der Charakterisierung von Hochfrequenzgeräten mit dem Vektor-Netzwerkanalysator
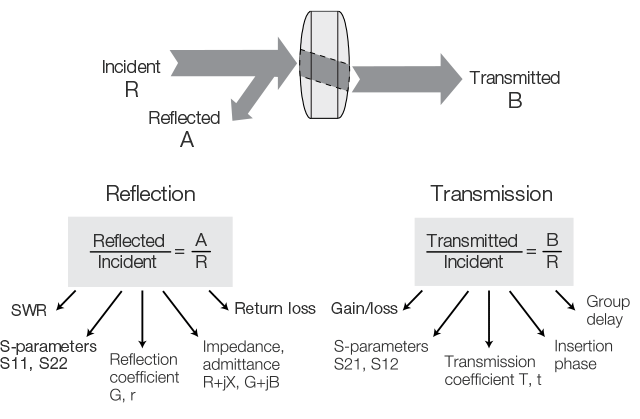
Die Charakterisierung von Niederfrequenzgeräten oder -netzen basiert in der Regel auf der Messung der H-, Y- und Z-Parameter. Dazu müssen die Gesamtspannung und der Gesamtstrom an den Eingängen oder Ausgängen des Geräts oder an den Knotenpunkten des Netzes gemessen werden, auch unter Leerlauf- und Kurzschlussbedingungen.
Bei höheren Frequenzen ist die Bestimmung der Gesamtspannung/des Gesamtstroms schwierig, sodass man hier die S-Parameter bevorzugt. Diese beziehen sich auf bekannte Messungen wie Verstärkung, Dämpfung und Reflexionskoeffizient, die ohne den Anschluss von unerwünschten Lasten an das Messobjekt möglich sind. Die S-Parameter mehrerer Komponenten können kaskadiert werden, um die Leistung eines Gesamtsystems vorauszusagen. S-Parameter können sowohl in linearen als auch in nichtlinearen CAE-Schaltungssimulationstools verwendet werden. H-, Y- und Z-Parameter können bei Bedarf aus S-Parametern abgeleitet werden.
Die Anzahl der S-Parameter für einen bestimmten Prüfling ist gleich dem Quadrat der Anzahl seiner Anschlüsse. Ein Gerät mit zwei Anschlüssen hat zum Beispiel vier S-Parameter: S11, S12, S21 und S22. Gemäß der Nomenklatur der S-Parameter beschreibt die erste Zahl den Anschluss, an dem die Energie austritt. Die zweite Ziffer zeigt den Anschluss an, an dem die Energie eintritt.
Beispiel: Der S-Parameter S21 beschreibt die Energie, die an Anschluss 2 austritt, wenn ein HF-Stimulus an Anschluss 1 angelegt wird. Sind die Zahlen gleich (z. B. S11), handelt es sich um eine Reflexionsmessung.
Abb.: S-Parameter eines Prüflings mit zwei Anschlüssen
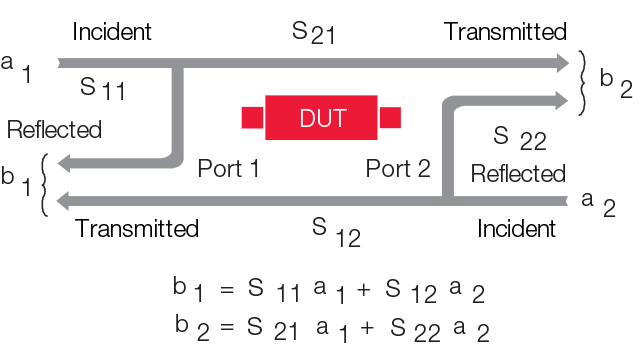
Die Streuparameter geben Aufschluss darüber, welche Signalanteile übertragen werden und wie hoch die reflektierten Anteile sind. Sie sind Kenngrößen, die das lineare Verhalten eines Prüflings beschreiben. S-Parameter lassen sich für weitergehende Simulationen nutzen.
S-Parameter S11: Der Eingangs-Reflexionsfaktor gibt Auskunft über die Anpassung der Signalquelle an die Schaltung.
S-Parameter S22: Der Ausgangs-Reflexionsfaktor bietet Aufschluss über die Anpassung des Ausgangs an den Eingang einer nachfolgenden Schaltung.
S-Parameter S21: Der Transmissionsfaktor ist gleichbedeutend mit der Verstärkung oder Dämpfung des Signals durch die zu messende Schaltung.
S-Parameter S12:Der Rücktransformationsfaktor gibt Auskunft über den Signalanteil, der vom Ausgang der zu testenden Schaltung an deren Eingang reflektiert wird.
Mit Hilfe von Verhältnismessungen können wir Reflexions- und Transmissionsmessungen durchführen, die sowohl von der absoluten Leistung als auch von den Änderungen der Quellenleistung gegenüber der Frequenz unabhängig sind. Die verhältnismäßige Reflexion (= Reflexionskoeffizient) wird oft als A/R und die verhältnismäßige Transmission als B/R dargestellt, was sich auf die Messkanäle bezieht. Der Reflexionskoeffizient ist das Amplitudenverhältnis zwischen reflektierter und einfallender Signalspannung.
Die Rückflussdämpfung (engl. RL, return loss) ist eine Methode, um den Reflexionskoeffizienten in logarithmischer Form (in dB) darzustellen. Die Rückflussdämpfung ist die Anzahl der Dezibel, um die das reflektierte Signal unter dem einfallenden Signal liegt. Die Rückflussdämpfung wird immer als positive Zahl ausgedrückt und variiert zwischen unendlich für eine Last mit der vorliegenden Wellenimpedanz und 0 dB bei einem Kurzschluss oder offenen Stromkreis.
Die Rückflussdämpfung steht im unmittelbaren Zusammenhang mit dem Stehwellenverhältnis (engl. VSWR, voltage standing wave ratio). VSWR ist definiert als das Verhältnis der Maximalspannung zur Minimalspannung in einem Stehwellen-Muster. Der VSWR-Wert reicht von 1 (keine Reflexion) bis unendlich (vollständige Reflexion).
Der Transmissionskoeffizient wird definiert als die übertragene Spannung geteilt durch die einfallende Spannung. Ist der Absolutwert der übertragenen Spannung größer als der Absolutwert der einfallenden Spannung, spricht man von einer Verstärkung des Prüflings oder Systems. Ist die übertragene Spannung kleiner als die einfallende Spannung, spricht man von einer Dämpfung oder Einfügedämpfung.
Stationäre Netzwerkanalysatoren (Benchtop- oder Desktop-Analysatoren) sind in der Regel sehr leistungsstarke, universell einsetzbare Geräte. Sie bieten eine hohe Messgenauigkeit und Messgeschwindigkeit sowie einen weiten Frequenzbereich. Hochwertige Desktop-Analysatoren überzeugen zudem durch ihre hohe Dynamik und Ausgangsleistung und durch niedrige Rauschwerte. Sie eignen sich optimal für die Entwicklung und Produktion von HF-Komponenten und kommen z. B. in der Kommunikations- und Elektronikindustrie, zur Designverifizierung von digitalen High-Speed-Leiterplatten oder für Anwendungen in der Luft- und Raumfahrt zum Einsatz. Dazu gehören auch sogenannte USB-Netzwerk-Analysatoren (VNA), welche die die Leistung und Präzision hochwertiger Desktop-VNA mit der Flexibilität mobiler Network-Analyzer vereinen.
Zu unseren stationären Netzwerkanalysatoren
Handheld-Analysatoren sind besonders robust, leicht bedienbar und speziell die für den Feldeinsatz konzipiert, z. B. im Servicebereich oder bei der Installation und Wartung von Antennenanlagen. In der Regel handelt es sich um multifunktionale Kombinationsgeräte für vielfältige Messanwendungen, z. B. als Netzwerkanalysator, Spektrumanalysator, Kabel- und Antennenanalysator oder HF-Leistungsmessgerät. Aufgrund der kompakten Bauweise und umfangreichen Funktionen müssen gegebenenfalls Abstriche bei der Leistung gemacht werden.
Sie sind sich noch nicht ganz sicher oder haben weitere Fragen zu den Geräten? Zögern Sie nicht uns zu kontaktieren. Ob direkt am Telefon oder per Online-Demo bequem bei Ihnen vor dem Bildschirm – Unsere Experten sind für Sie da.